首页 C&C++ 数据结构与算法分析

# 编写个程序执行对一个图的拓扑排序

拓扑排序简单的来说是求有向无环图的一条从顶点vv 到顶点uu 的路径。

拓扑排序参考链接
/*
-----    -----
| 1 | -> | 2 |
-----    -----
  |   \   /|\
 \ /  _\/  |
-----    ----- 
| 4 |    | 3 |
-----    -----
 / \  \     |
  |   _\/  \|/
-----     -----  
| 6 | ->  | 5 |
-----     -----  
*/
void Topological_Sort(Graph G)
{
    /*
    * Create an array of in-degrees for each vertex
    * and statistics
    * Note: if your camke project build in VS, you should
    * use int indegree[10] replace int indegree[G->Vertex_Num]
    * otherwise it will fail build
    */
    int indegree[10];
    // int indegree[G->Vertex_Num];
    FindIndegree(G, indegree);
    
    // Init stack
    Stack S = Stack_Init();
    
    // Find vertex for zero indegree and push it onto the stack
    for(int i = 0; i < G->Vertex_Num; i++)
    {
        if(!indegree[i]) Push(S, i);
    }
    int index,count = 0;
    while(!Stack_IsEmpty(S))
    {
        index = Pop(S);
        printf("%d ",G->Vertices[index].Data);
        ++count;
        
        for(Arc_Node p = G->Vertices[index].First_Adj; p!=NULL; p = p->Arc_Next)
        {
            vertex_type k = p->Adj_Index;
            if(!(--indegree[k])) Push(S,k);
        }
    }
    // Free stack
    free(S);
    if(count<G->Vertex_Num) 
      printf("该图有回路\n");
}
# 使用标准的二重循坏，一个邻接矩阵仪初始化就需0(∣V∣2)0(|V|^2)。试提出一种方法将一个图存储在一个邻接矩阵中（使得测试一条边是否存在花费O(1)O(1)）但避免二次的运行时间。
在图已知的情况下，使用散列表映射图的下标可以实现，这样可以避免标准的二重循环。
# 当用 d - 堆实现时，Dijkstra 算法最坏情形的运行时间是多少？
假设使用 d - 堆实现 Dijkstra 算法时，则对于对于DecreaseKeyDecreaseKey 每次花费O(log⁡d∣V∣)O(\log_d{|V|}), 总共∣E∣|E| 次；对于DeleteMinDeleteMin 则每次花费O(dlog⁡d∣V∣)O(d\log_d{|V|}), 总共∣V∣|V| 次，所以总的运行时间是O(∣E∣log⁡d∣V∣+∣V∣dlogd∣V∣)O(|E|\log_d{|V|} + |V|dlog_d{|V|})。但是当d=∣E∣/∣V∣d = |E|/|V|, 对于稀疏图而言，它的运行时间要比d=2d=2 还要多，所以dd 最好的范围为max(2,∣E∣/∣V∣)max(2,|E|/|V|)。
# 给出在有一条负边但无负值圈时 Diklra 算法得到错误答案的例子。
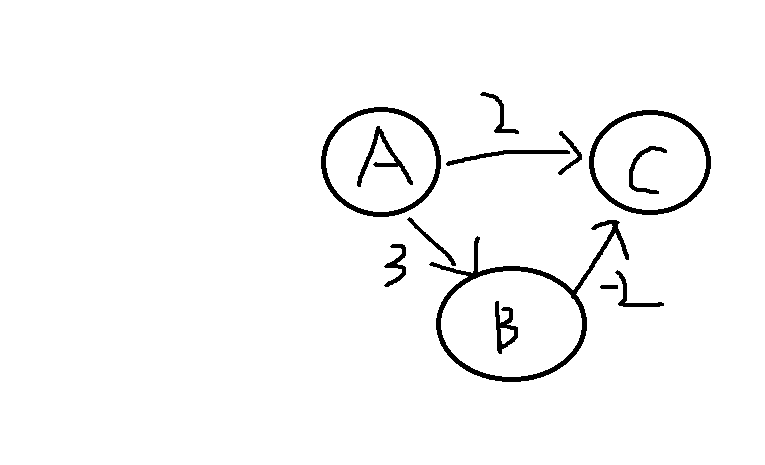
# 证明，如果存在负权边但无负值圈，则 9.3.3 段中提出的赋权最短路径算法是成立的，证明该算法的运行时间为O(∣E∣⋅∣V∣)O(|E|·|V|)。
使用一个队列存储vv 个顶点，能较快速实现查找操作，同时实现EE 次边的查找，忽略常数时间的话，则总的运行时间为O(∣E∣⋅∣V∣)O(|E|·|V|)。
# 设一个图的所有边的权都在11 和∣E∣|E| 之间的整数。Dijkstra 算法可以多快实现？
Dijkstra 算法最坏情形下的运行时间是O(E+V2)O(E+V^2), 当EE 很大时，运行时间为O(E+V2)O(E+V^2)，当EE 很小时，运行时间为O(Elog⁡v)O(E\log{v})。
# 写出一个程序来求解单发点最短路径问题。
其实就是叫你写出 Dijkstra 算法。
void Dijkstra(Table T)
{   
    for(int Cur_Index= SmallDistance(T);Cur_Index != NotVertex; 
        Cur_Index= SmallDistance(T))
    {
        T[Cur_Index].Known = true;
        int Com_Index;//Compare the distance of vertex between the adjacency list
        for(List P = T[Cur_Index].Header; P != NULL; P = P->Next)
        {
            Com_Index = Find_Index(T,P->Data);
            if(!T[Com_Index].Known)
            {
                if(T[Cur_Index].Distance+P->Weight<T[Com_Index].Distance)
                {
                    T[Com_Index].Distance = T[Cur_Index].Distance + P->Weight;
                    T[Com_Index].Path = Cur_Index;
                }
            }
        }
    }
}
# 解释如何修改 Dijkstra 算法以得到从vv 到ww 的不同的最小路径的个数的计数。
使用path[]path[] 计数并存储路径，并加个countcount 记录路径个数。
# 解释如何修改 Dijkstra 算法使得如果存在多于一条从vv 到ww 的最小路径，那么具有最少边数的路径将被选中。
在上个问题的基础上 (就是上面那个) 建立一个边数统计数组，当dv+Cv,w=dwd_v + C_{v,w} = d_w，选择最小的路径，否则清除之前得到的路径，保留之前的路径。
# 设G=(V,E)G=(V,E) 是一棵树，ss 是它的根，并且添加一个顶点tt 以及从GG 中所有树叶到tt 的无穷容量的边。给出一个线性时间算法以找出从ss 到tt 的最大流。
从根节点开始，一直递归至叶子，期间
如果是叶子，则返回流；
如果不是叶子，继续递归进入子树，直至查找到对应的叶子或非叶子tt；
找到时进入流，并减去权重，逐级计算直到SS。
# 一个二分图G=(V,E)G=(V,E) 是把VV 划分成两个子集V1V_1 和V2V_2 并且其边的两个顶点都不在同一个子集中的图。
# 给出一个线性算法以确定一个图是否是二分图。
设全部顶点未标记，寻找任意顶点，找到则先标记为红色，之后使用深度优先搜索搜索连接的下一个顶点，标记为蓝色，与此同时：
若检测有不在红蓝之间的线，则非二分图，退出；
若是，则继续验证，若遇到不连通的点，寻找新点继续验证，直至全部验证完退出。
# 证明网络流问题可以用来解决二分匹配问题。
二分图顶部加一个顶点ss 至所有的边，即vv 至ww，同理，底部加一个顶点tt 至所有的边，同时给所有的边加上权重weight∈(1,S]weight\in (1,S], 这样，一个二分图就可以转换为网络流最大匹配问题。
# 给出一个算法找出容许最大流通过的增长通路
只需要对 Dijkstra 算法进行轻微修改即可。原始的 Dijkstra 算法在未标记顶点时设置路径全为∞\infty, 则找最大流只需要设置未标记顶点时距离全为00, 之后的步骤就和正常的 Dijkstra 算法一样。
# 证明VV 个顶点的图可以有Vv−2V^{v-2} 棵最小生成树。
假设存在所有边权重为 1 的无向图，假设v=2v=2, 则只有11 棵最小生成树，当v=3v=3, 则只有33−2=33^{3-2}=3 棵最小生成树，那么继续往下递增，则可以得出归纳VV 个预点的图可以有Vv−2V^{v-2} 棵最小生成树。
# 编写一个程序实现 Kruskal 算法。
Edge Kruskal(Edge G)
{
    Edge MinTree = malloc(sizeof(_Edge));
    MinTree_Init(G, MinTree);
    DisjSet S;
    DisjSet_Init(S);
    SetType Uset, Vset;
    // You can also use heap sort
    qsort(G->Edge,G->Edge_Num,sizeof(G->Edge[0]),Compare);
    for(int i = 0; i < G->Edge_Num; i++)
    {
        /*
        * The function of the union check is to confirm 
        * whether the vertices are in the same subtree, 
        * and merge if not.
        */
        Uset = Find(G->Edge[i].inital,S);
        Vset = Find(G->Edge[i].end,S);
        if(Uset != Vset)
        {
            MinTree->Edge[MinTree->Edge_Num++] = G->Edge[i];
            Union(S,Uset,Vset);
        }
        if(MinTree->Edge_Num ==G->Vertex_Num-1) break;
    }
    return MinTree;
}
# 如果一个图的所有边的权都在11 和∣E∣|E| 之间，那么能有多快算出最小生成树？
Kruskal 算法的主要运行时间在并查集的合并和排序的查找，并查集无法更改，排序可以尽可能快，目前用桶排序加并查集的总运行时间能达到O(∣E∣+∣V∣log⁡∣V∣/log⁡log⁡∣V∣)O(|E|+|V|\log{|V|/\log{\log|V|}})。